Wallpaper groups. Portuguese tiles: A contribution for a mathematical classification of square tiles

A contribution for a mathematical classification of square tiles
Download: PDF Other formats

Jorge Rezende

In this article we study some geometric properties of a non-trivial square tile (a non-trivial square tile is a non-constant function on a square).

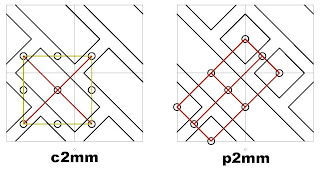
Consider infinitely many copies of this single square tile and cover the plane with them, without gaps and without overlaps (a tiling of the plane), with the vertices making a square point lattice. The question we ask ourselves in this article is the following: if there is a rotation center of order 4 what kind of geometric properties has the drawing in the tile?

We prove that the tiles of this kind that one can see belong to one of four types. However, there are eight exceptions to these general rules.

This work was inspired by a pattern tile, with remarkable properties, designed in 1966 by the portuguese artist Eduardo Nery. It can be seen in many beautiful panels in several locations in Portugal.

-

Acknowledgements 

-

For scientific support:

 http://gfm.cii.fc.ul.pt/

-

For technical support: 

http://artenumerica.com/