Reflexões sobre os "Estudos para um azulejo de Eduardo Nery"

O azulejo das figuras 1 é o de Eduardo Nery. Os outros dois azulejos são azulejos em que eu desenhei 3 letras: F, P, R. Estas três letras são boas para isto porque não têm simetrias de qualquer espécie.

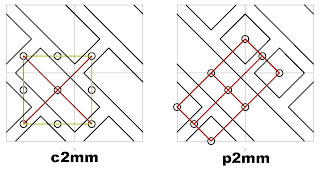
As linhas vermelhas representam eixos de reflexão. As verdes, representam eixos de reflexão deslizante. Os pontos com um 2, representam centros de rotação de ordem 2. A fronteira das regiões fundamentais é assinalada com linhas amarelas, quando não coincida com eixos de reflexão.

A figura 2a representa um azulejo com as condições necessárias e suficientes, para num painel de tipo 28 ter um grupo como o azulejo de E. Nery. Há um eixo de reflexão numa diagonal. Dividi o azulejo em 4 quadrados iguais. No centro de cada um dos quadrados há um centro de rotação de ordem 2. Dois dos quadrados têm mais um eixo de eixo de reflexão numa diagonal. O resultado é que o painel de tipo 28 tem o mesmo grupo que o azulejo de E. Nery (Figura 2b). No painel de tipo 58 não tem o mesmo grupo (Figura 2c). Logo, o azulejo 2 não é matematicamente equivalente ao de E. Nery.

A figura 3a representa um azulejo com as condições necessárias e suficientes, para num painel de tipo 58, ter um grupo como o azulejo de E. Nery. Há um eixo de reflexão numa diagonal. Dividi o azulejo em 4 quadrados iguais. No centro de dois dos quadrados há um centro de rotação de ordem 2. Os 4 quadrados têm mais um eixo de eixo de relexão numa diagonal. O resultado é que o painel de tipo 58 tem o mesmo grupo que o azulejo de E. Nery (Figura 3c). No painel de tipo 28 não tem o mesmo grupo (Figura 3b). Logo, o azulejo 3 não é matematicamente equivalente ao de E. Nery.

De facto, o azulejo de E. Nery tem as propriedades acumuladas do azulejo 2 e do azulejo 3.

O azulejo de Setúbal de E. Nery é ainda matematicamente distinto destes três.

Tudo isto coloca muitas interrogações como a da classificação matemática dos azulejos. Assim vejo uma das formas como o azulejo de Eduardo Nery me interpela.

(Adaptação de um texto de 29 de Novembro de 2011)

Nota de 30 de Junho de 2012: Como se vê não há aqui, ainda, qualquer referência ao painel de tipo 38, referência preferencial que se dá no artigo que, a seguir, se cita.

-

See: 
A contribution for a mathematical classification of square tiles
Download: PDF Other formats 
Jorge Rezende
-
Video: 
The magic of a Eduardo Nery tile
- 
See also: 
Estudos para um azulejo de Eduardo Nery 
História de um azulejo de Eduardo Nery

The magic of a Eduardo Nery tile

Video:

The magic of a Eduardo Nery tile

-

See:

A contribution for a mathematical classification of square tiles
Download: PDF Other formats

Jorge Rezende

-

See also:

Estudos para um azulejo de Eduardo Nery

História de um azulejo de Eduardo Nery

The magic of a Eduardo Nery tile (trailer)

-

This video can also be seen here:

The magic of a Eduardo Nery tile (trailer) 

-

See:

A contribution for a mathematical classification of square tiles
Download: PDF Other formats

Jorge Rezende

-

See also:

Estudos para um azulejo de Eduardo Nery

História de um azulejo de Eduardo Nery

Estudos para um azulejo de Eduardo Nery (esquemas)

Azulejo de Eduardo Nery

-

Estes esquemas foram realizados pelo autor deste blogue entre 10 e 19 de Julho de 2011.
O meu plano inicial era desenhar/ver todas as pavimentações do plano com o azulejo de Eduardo Nery com uma região fundamental com área menor ou igual a 4 (azulejos).

Uma das possiblidades é a de reunir os 4 azulejos em torno de um dos vértices.

Em primeiro lugar, numerei os vértices no sentido directo (o contrário ao dos ponteiros do relógio): 1, 2, 3 e 4. Reservei os números ímpares (1 e 3) para os vértices que contêm a diagonal que é um eixo de refexão do azulejo. Os pares (2 e 4) têm a diagional amarela. O 1 é o vértice que só tem como canto o triângulo amarelo.

Fixei de uma vez por todas um azulejo. Depois, para cada um dos três restantes há quatro possibilidades. O que dá 64 (4x4x4) possibilidades. Imaginemos o número brutal de possibilidades se em vez de 4 fossem 9, por exemplo... (dava 16x16x16x16(=65536)).

Depois, tratava-se de fazer as translacções. Nas figuras estão representadas 6 imagens, correspondentes a 6 páginas. Na última figurinha de cada página, a vermelho, estão desenhados os vectores que fazem as translacções. Há 3 possibilidades o que dá 3x64. Páginas 1 e 2: vectores ortogonais, com comprimento 2, paralelos aos lados dos azulejos. Páginas 3, 4, 5 e 6: vectores oblíquos.

Tudo feito, há muitas repetições e equivalências (são numeradas e notadas a verde). Por exemplo, as páginas 5 e 6 são meras repetições.

As imagens dos "Estudos" correspondem ao resultado final. Há 36 possibilidades, contadas assim:

a) Páginas 1 e 2:

Com reflexão: 1, 3, 8, 11, 14, 20, 23, 28, 35, 38, 58.

Sem reflexão: 2, 6, 7, 10, 18, 19; não desenhei os desenhos reflectidos, considerei-os equivalentes; quem os quiser ver, basta pôr estes ao espelho...

Ao todo: 17

b) Páginas 3 e 4:

Com reflexão: 1', 8', 14', 41', 53'.

Sem reflexão: 2', 3', 4', 6', 7', 10', 19', 20', 21', 25', 35', 36', 42', 52'; mais uma vez, não desenhei os desenhos reflectidos.

Ao todo: 19

Nos esquemas finais, estão resumidos, nas páginas 7-9, os (36=17+19) desenhos destas possibilidades. São estes os "Estudos para um azulejo de Eduardo Nery".

As restantes possibilidades estão resumidas nas páginas 10 e 11. São 24. Não fiz desenhos como fiz para os "Estudos".

O que mais me surpreendeu, na altura, foi o desenho 58. No caso Contumil / Mértola / Torres Vedras é do grupo p2mm e a sua região fundamental (cujo esquema está aqui) tem a área 1 (a área de 1 azulejo). No caso Setúbal é do grupo p2mg e a sua região fundamental (cujo esquema está aqui) tem a área 2 (a área de 2 azulejos).

Nos esquemas finais (páginas 7-9), como se pode ver, escrevi a lápis os grupos, por "palpite", antes de fazer os desenhos. Grande ingenuidade!... Feitos os desenhos ("Estudos para um azulejo de Eduardo Nery") verifiquei que estava enganado. 

(Adaptação de um texto de 13 de Novembro de 2011)

Página 1

Página 2

Página 3

Página 4

Página 5

Página 6

Página 7

Página 8

Página 9

Página 10

 

Página 11

-

Ver:

Todos os estudos para um azulejo de Eduardo Nery

Todos os estudos para um azulejo de Eduardo Nery

Estudos para um azulejo de Eduardo Nery: 1, 3, 8, 11, 14 e 20

Estudos para um azulejo de Eduardo Nery: 23, 28, 35, 38, 58 e 2

Estudos para um azulejo de Eduardo Nery: 6, 7, 10, 18, 19 e 1'

Estudos para um azulejo de Eduardo Nery: 8', 14', 41', 53', 2' e 3'

Estudos para um azulejo de Eduardo Nery: 4', 6', 7', 10', 19' e 20'

Estudos para um azulejo de Eduardo Nery: 21', 25', 35', 36', 42' e 52'

-

Estes "estudos" foram realizados pelo autor deste blogue entre 20 e 22 de Julho de 2011

-

See:

A contribution for a mathematical classification of square tiles
Download: PDF Other formats

Jorge Rezende

-

See also:

Estudos para um azulejo de Eduardo Nery

História de um azulejo de Eduardo Nery

Symmetries of a Eduardo Nery tile

 We represent rotation centers of order 4 by small black squares; those of order 2 by small circles; reflections are represented by red lines.

 -

See:

A contribution for a mathematical classification of square tiles
Download: PDF Other formats

Jorge Rezende

-

See also:

Estudos para um azulejo de Eduardo Nery

História de um azulejo de Eduardo Nery

Wallpaper groups. Portuguese tiles: A contribution for a mathematical classification of square tiles

A contribution for a mathematical classification of square tiles
Download: PDF Other formats

Jorge Rezende

In this article we study some geometric properties of a non-trivial square tile (a non-trivial square tile is a non-constant function on a square).

Consider infinitely many copies of this single square tile and cover the plane with them, without gaps and without overlaps (a tiling of the plane), with the vertices making a square point lattice. The question we ask ourselves in this article is the following: if there is a rotation center of order 4 what kind of geometric properties has the drawing in the tile?

We prove that the tiles of this kind that one can see belong to one of four types. However, there are eight exceptions to these general rules.

This work was inspired by a pattern tile, with remarkable properties, designed in 1966 by the portuguese artist Eduardo Nery. It can be seen in many beautiful panels in several locations in Portugal.

-

Acknowledgements 

-

For scientific support:

 http://gfm.cii.fc.ul.pt/

-

For technical support: 

http://artenumerica.com/

Estudos para um azulejo de Eduardo Nery: 1, 3, 8, 11, 14 e 20

1 - p4mm

3 - cm

8 - pm

11 - cm

14 - p2mg

20 - cm

Estes "estudos" foram realizados pelo autor deste blogue entre 20 e 22 de Julho de 2011

Portuguese pavements. Eduardo Nery: Pavimentos no Edifício Comercial na Rua Braamcamp, nº 9, em Lisboa, 1967/69

Pavimentos no Edifício Comercial na Rua Braamcamp, nº 9, em Lisboa, 1967/69

No pavimento da cave, executado em “calçada-mosaico” em preto e branco, procurei organizar uma grande variedade de combinações a partir apenas de 4 círculos com diâmetros diferentes, tendo procurado obter os seguintes objectivos:
- Criar um percurso variado e coerente, ao longo da galeria da cave;
- Exprimir através do desenho do chão a possibilidade de escolha do caminho, em especial na bifurcação a meio da galeria, que dá acesso à caixa da escada interior do prédio;
- Distribuir o claro-escuro do pavimento por forma a contrariar e “corrigir” no chão os triângulos de sombra provocados pelos pilares da construção: - usando maior percentagem de branco nessas zonas de sombra, e mais preto nas áreas que recebem mais luz natural;
- Quanto ao desenho nos vários padrões de círculos, usei-o com ritmos diferentes. Diversas combinações dos quatro moldes dos calceteiros permitiram-me inscrever círculos mais pequenos em círculos maiores, criando assim ritmos de crescimento e de decrescimento do claro-escuro, e do próprio desenho.
Usei também círculos negros sobre fundo branco, e círculos brancos sobre fundo branco, servindo-me neste último caso do corte das pedras para salientar os círculos brancos.
- Nos patins das escadas, ao mesmo nível da rua, preocupei-me sobretudo em relacionar o pavimento da calçada com o desenho de linhas rectas dos labirintos em betão aparente, que projectei para as duas empenas do prédio.
Mas também aqui procurei diferenciar a entrada dos automóveis para o monta cargas, assinalada por uma barra larga perpendicular ao portão da garagem, em oposição com o percurso das pessoas, que é mais livre e dinâmico.

Eduardo Nery

[O autor deste blogue agradece a Eduardo Nery a autorização para publicar estes seus documentos (texto e fotos)]

-

Edifício "Franjinhas" - Rua Braamcamp, nº 9

Arquitectos Nuno Teotónio Pereira e João Braula Reis (1971 – Prémio Valmor)

Foto de Fernanda Garrido